Practice working on specific math concepts with our set of 5 printable math graphic organizers.
Help Struggling Students with Math Graphic Organizers!
Graphic organizers are an essential tool in mathematics, specifically for young learners. Their visual framework greatly enhances comprehension and learning of otherwise abstract concepts. With these tools, students can categorize information, identify patterns, and establish relationships between mathematical ideas, developing logical reasoning and spatial awareness. This helps our youngest students grasp more complex math concepts quickly, laying a solid foundation for future success. In mathematics education, incorporating high-quality visual organization tools can be a total game-changer.
Pick a Printable Graphic Organizer for Math!
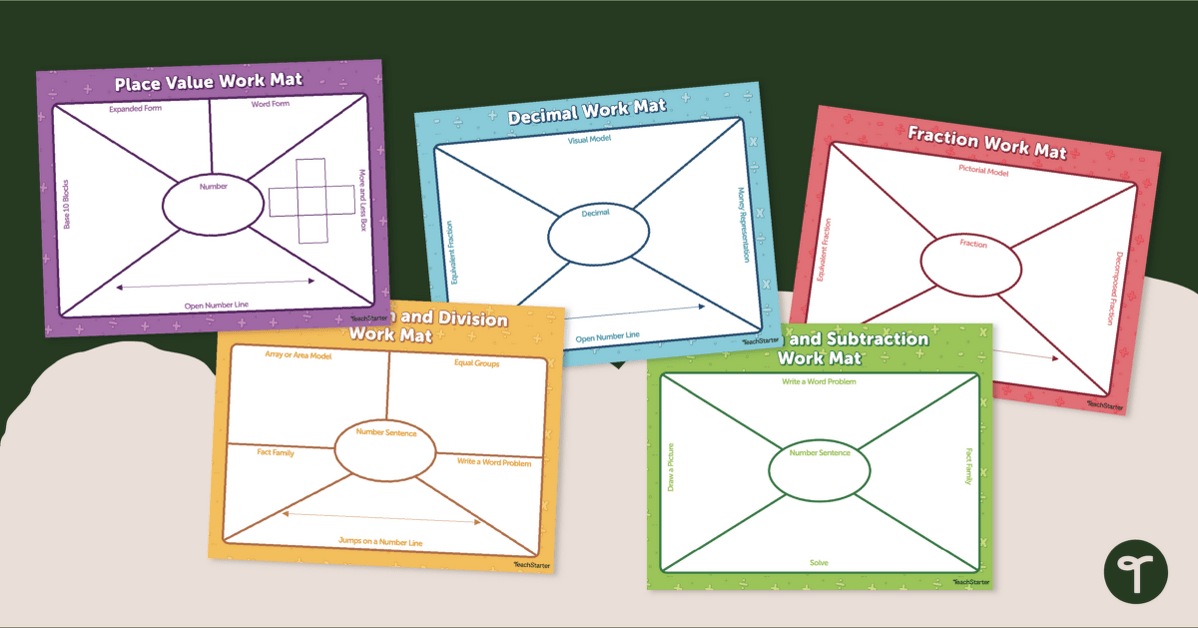
Use these work mats in your math class when working on the concepts of:
- place value
- addition and subtraction
- multiplication and division
- fractions
- decimals.
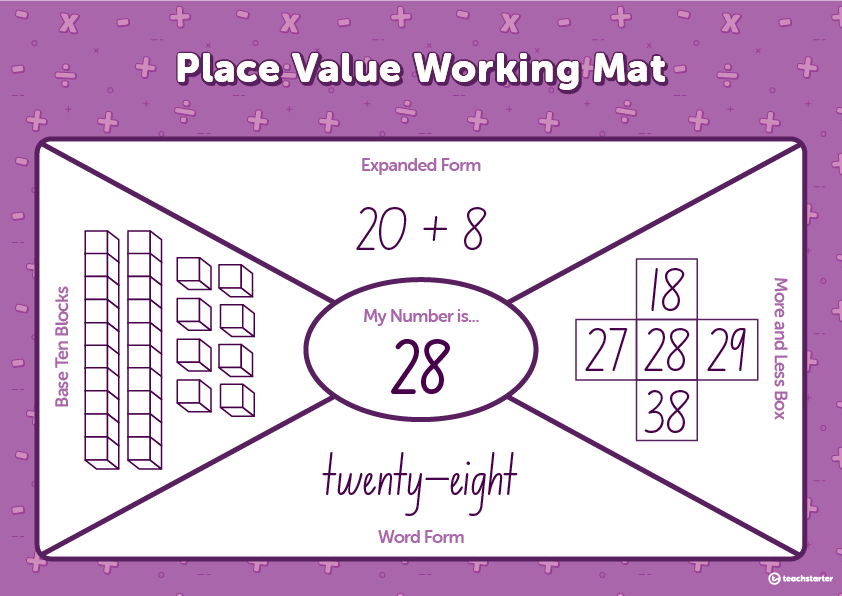
Each work mat has the students complete a series of tasks associated with that concept. These work mats are great to use with your guided math groups and when put in a math center. Simply slip a copy in a dry-erase sleeve so that your students can use a dry-erase marker and then wipe it clean.
Alternatively, project a copy on your dry-erase board to use as a whole class math warm-up.
Use the drop-down menu to choose between the color or black-and-white versions. This resource downloads as a PDF.










0 Comments
Write a review to help other teachers and parents like yourself. If you'd like to request a change to this resource, or report an error, select the corresponding tab above.